受験算数について

※昨年度の記事を一部改訂のうえで再掲載いたします。ご参考にしていただければ幸いです。

◆受験算数入門

さて今回の話題は多くの中学受験生の頭を悩ます「受験算数」です。保護者の皆様も多くの方が教えるのを諦めていらっしゃるのではないでしょうか。

この受験算数を特徴づけるもののひとつが「特殊算」といわれる問題群です。「和差算」「つるかめ算」「旅人算」「消去算」「差集め算」等々お聞きになったことがある方も多いのではないでしょうか。実はこれらの多くが中学に入ると方程式に置き換わっていきます。ですから保護者の方の多くが手こずるのも故なきことではありません。大人は例外なく数学の洗礼を受けていますから…。例えば以下のような問題を解くとき保護者の皆さんは、間違いなく方程式を立てて解いていきますよね。

1本80円の鉛筆と1本120円のボールペンを合わせて15本買ったら1400円でした。それぞれ何本買ったでしょう。

ところが、小学生は方程式など知りませんから、これを算数で解いていかねばなりません。

やってみましょう。

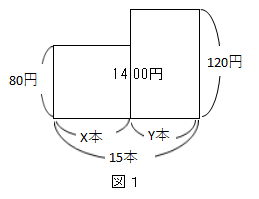先ず、図１のように考えます。80円の鉛筆x本と120円のボールペンy本の値段を長方形の面積に置き換えます。これの合計が1400円。
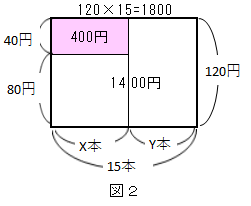次に図2のように、120円15本の面積（1800円）を考え、先ほどの1400円との差を取ります。図の左上の400円の面積になりますね。　

この400円の面積の縦の長さは120円と80円の差の40円になりますから、x=400÷40=10が80円の鉛筆の本数になります。yは15から引けばOKですね。なんて巧妙なやり方でしょう！

これは面積図という手法ですが、特殊算を解いていくためには面積図の他にもいろいろな手法があります。線分図を使ったり、あるいはグラフを描き、表を作り、場合によっては数学もどきの式を使って、と様々な方法を駆使します。

さらには、ひとつの問題に対してもいろいろなアプローチがあります。

例えば、こんな問題。

ある池の周りに5m間隔で木を植えると、7m間隔で植えるより8本多く植えることができました。この池の周りの長さを求めなさい。

【解法①】
7m間隔で5m間隔のときと同じ本数を植えたとします。そうすると7m間隔の方が周囲が7×8=56m長くなりますね。ひとつの間隔辺り2mの差があるのですから、これは56÷2=28本分の差であったことが分かります。つまり5m間隔で28本の木が植えられていたことが分かり、周りの長さは5×28=140mと分かります。

これが差集め算と云う解き方。

【解法②】
7mと5mの最小公倍数を考えると35mですね。周囲が35mの池を考えると、7m間隔では35÷7=5本、5m間隔では35÷5=7本の木をうえることができ、その差は２本です。実際には差は8本だというのですから周囲の長さは35mの4倍(=8÷2)の長さだったと分かります。つまり35×4=140mとなるわけです。

こんな風に整数の問題として解くことも出来ます。

このようにひとつの問題にも複数のアプローチの仕方がある場合も結構あります。どの解き方が一番良いと云うわけではありません。自分の得意技を作っていきましょう。

また、上記のことからも何となくお分かりいただけると思いますが、算数は数学に比べて、意味が分かっていないと解けない、と云う側面が強いことが分かります。方程式は式さえできてしまえば、あとは形式的に解くだけです。意味なんか分からなくても解けます（チョット乱暴ですが^^）。しかし、算数はそういう訳にはいきません。いま自分は何をどう考えて、何について計算しているのかを常に意識しなければならないのです。これは私立中学の先生方が受験生に「意味考えてね」というメッセージを送っているのですね。

 

◆受験算数の通奏低音「比」

さて算数の問題には特殊算以外にもいろいろな問題があるのですが、受験算数の通奏低音は「比」です。

上記のいろいろな特殊算も、特殊算そのものは実はそんなに難しいものではないことが多いのです。ところがここに一旦「比」が入ってくると、途端に難度が上がります。そしてこの「比」は受験算数のどの分野にもそっと忍び込んでくるのです。

以下では「比」を使って解く問題をいくつかご紹介しましょう。

難関校の算数の問題には大変込み入った難しい問題も多いのですが、今日のところは解説されれば「ああそうか」となる程度の問題をご紹介しますので、算数の苦手な方もどうぞお付き合いください。

【速さと比】
先ず定番の速さと比です。道のり=速さ×時間ですから、道のりが同じ場合、速さと時間は反比例の関係になります。この考え方は大変良く使われる手法です。入試問題を例に挙げます。

ある道のりを進むのに分速60mで歩く場合と分速52mで歩いた場合では40秒の差がありました。この道のりは何mですか。（吉祥女子）
【解法】
道のりが一定ですので、速さと時間は反比例します。よって速さの比と時間の比は逆比（逆数の比）になります。速さの比が60:52=15:13ですから、時間の比は1/15:1/13=13:15となります。この差は比で表すと2でこれが40秒に相当します。よって比の13に相当する時間は40×(13/2)=260（秒）＝260/60（分）。つまり分速60ｍで260/60（分）かかる道のりだから、60×(260/60)=260ｍと云うことになります。

この問題は差集め算でも解けますが、このように比を使った解法がお勧めです。

【仕事算と比】
仕事算と云う問題群があります。ここでも比を使った解法が威力を発揮します

ある仕事を1人で行うと、Aさんは16日、Bさんは24日、Cさんは18日かかります。この仕事を3人で始めましたが、Aさんが途中から休んだため、仕事を終えるのにちょうど9日かかりました。Aさんが休んだ日数は何日ですか。（日大二中）

【解法】
まずAさん、Bさん、Cさんの1日あたりの仕事の比を求めるとA：B：C＝1/16：1/24：1/18=9:6:8となります。

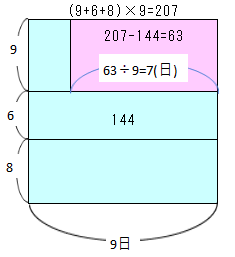そこでAさんが9、Ｂさんが6、Ｃさんが8の仕事をすることにします。そうすると仕事全体はＡさんが16日で仕上げるのですから9×16＝144となります（これは、ＢさんorＣさんで計算しても同じです）。
さて、ここでも面積図を使ってみましょう。
A、B、Cの1日あたりの仕事を縦に取り、横軸に日数を取ります。3人全員が9日働いたとすると207の仕事になりますが、実際は144です。その差63は図のピンクの部分になり、これはAの7日分に当たることが分かります。

よって、Aがお休みしたのは７日間と云うことになりますね。

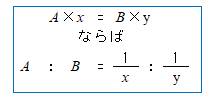上記の例では２つとも逆比を使いました。反比例の関係にある2数を扱うとき、一方の比が他方の逆比になると云う関係はぜひ身につけておきたい感覚です（右図を参照してください）。
このように、比に関連して比例・反比例の考え方もしっかり身につけておきたい概念です。これは理科の計算問題を解くときにもとても役に立ちます。
 

【図形への利用】

図形で最も難しいものはおそらく相似でしょう。
ちなみに高校受験では「相似」「三平方の定理」が図形の難関問題の双璧ですが、中学受験では「三平方」は出てきませんので、「相似」が最難関の問題を形成します。そしてこれもまた「比」の問題です。
ここでも入試問題を見てみましょう。

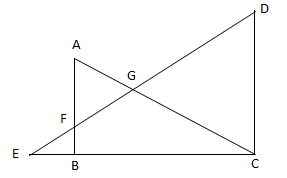右図のように2つの直角三角形ABCとDECが重なっています。EDとAB、ACの交わる点をそれぞれF、Gとします。
AF：FB：DC=3：1：5であるとき、三角形EBFと四角形BCGFの面積の比を求めなさい。（城北）

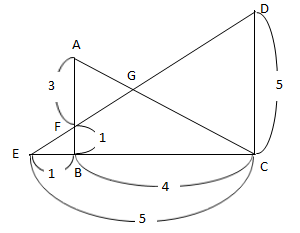この問題は、△EBFと△ECDは相似比1：5、△AFGと△CDGは相似比3：5の相似な三角形。△EBFと△CBF、△CFGと△CDGはそれぞれ高さの等しい三角形であることに着目して解いていきます。

つまり△EBF：△ECD＝1：25（面積比は相似比の2乗になることを利用します）、よって△EBF：四角形FBCD＝1：24。

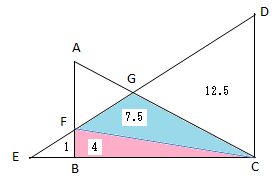
また△EBF：△CBF＝1：４なので、△CBF：△CFD＝4：20。△AFGと△CDGの相似比が3：５だからFG：GD＝3：5。よって△CFG=20×(3/8)=7.5。

上記をまとめると、三角形EBF：四角形BCGF=1：（4+7.5）=1：11.5＝2：23となります。

最後は少し乱暴な説明になってしまいましたが、比がいろんな形で様々な問題に関わってくることの一端に触れていただけたのではないかと思います。

比のお話の最後にあたって大事なことをもうひとつ。
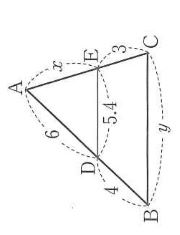
比の問題を考えていくとき、比を分数の形で追っかけることができるようになってください。

例えば右の図でxを求めたいとき、x：3=6：4と云う比例式を解くのではなく、x=3×(6/4)と分数を利用して解いていけるよう訓練しましょう。同様にyを求める時もy=5.4×(10/6)と解きたいところです。比は分数である、という感覚を身につけましょう。

 

さて今回は比がいろいろ問題に入り込んでくる様をご紹介する記事になりましたが、中学受験には様々な分野があります。もちろん比の考え方を使わずに解く問題もたくさんあります。

しかし中学受験生が問題を解くために持っている（持っておくべき）道具は、それほど千差万別と云うわけでもありません。最初の方でも少し触れましたが、線分図や面積図の利用、図や表を書いて整理する、式を立ててみるetcどんな問題にも適用できるスキルを使って解いていくことが非常に多いのです。

ですから大事なのは、それぞれの道具の使い方を理解して、しっかり磨きをかけておくことです。そして自分はどの道具を使うのが一番得意なのかを見定めておいてください。自分の道具箱の中身を充実させていってください。

受験生はこれから本格的な入試問題演習の時期に入っていきます。算数の問題を解いていくとき、何となく解くのではなく、自分の思考を跡付けながら自覚的に解いていきましょう。自分はこの問題をどう考えてどのような手順で解こうとしたのか。そしてそれがベストの考え方なのか。問題演習と反芻の繰り返しが、受験生の実力を大きく伸ばすハズです。